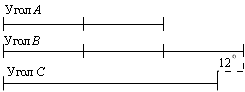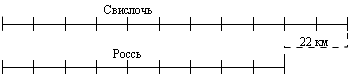Задачи, которые не были установлены
Задачи, которые нельзя установить, не меняя условия (или вообще нельзя установить)
В таблице 1 приведен список соответствующих задач учебника.
>>
Таблица 1
| Тип | Раздел | Номера |
| Задачи на объяснение | I | 39,63,
149, 205, 236, 297, 314,
315 |
| II | 417,437 |
| III | 589 |
| IV | 735, 789, 921 |
| Задачи на доказательство | I | 309 |
| III | 511, 512, 545,
555 |
| IV | 661, 694, 804 |
| Упражнения на составление задачи | I | 72 |
| III | 589 |
| Прочие | I | 298 |
| III | 496, 500, 619 |
Объясните, почему верно равенство:
а) 9349 + 82 047 = 82 047 + 9349;
б) (34789 + 2462) + 538 = 34789 + (2462 + 538);
в) 49 962 + 7058 = 50 000 + 7020.
Объясните, что означает:
а) вычесть число 158 из числа 858;
б) из числа 125 вычесть число 119;
в) вычесть из числа 48 721 число 121.
Составьте задачу, которая решается выражением:
а) 24 + (24 - 5);
б) 78*3 - 46*4.
Трое путешественников - Антон, Артём, Филипп - одновременно подошли к реке. У одного из них была надувная лодка, которая
выдерживает не больше 100 кг. Антон весит 46 кг, Артем - 39 кг, Филипп - 86 кг. Путешественники успешно переправились на другой
берег. Как они смогли это сделать?
Три человека смогли переправиться через реку, хотя лодка, которую они использовали, вмещает только одного. Как такое могло
произойти?
Измерьте все углы на рисунке. Сделайте вывод.
Трое рыбаков имеют общую лодку, и у каждого есть свой замок и ключ к нему. Как прикрепить лодку к берегу, чтобы каждый из
рыбаков мог ей пользоваться (открыв один замок одним ключом)?
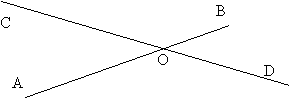
Три прямые - AB, CD, EF - пересекаются в одной точке O. Докажите, что РAOC
+ РFOD + РBOE =180o.
Найдите угол BOE, если известно, что РAOC+РFOD =148o.
С одной и той же станции в одно и то же время в противоположных направлениях выехали два автобуса. Скорость одного автобуса
40 км/ч, а второго - 50 км/ч. Какое расстояние будет между автобусами через b ч после отправления? Запишите ответ формулой.
Упростите её. Что означает число 90 в полученной формуле?
Из одного же населённого пункта в одном направлении вышли одновременно два пешехода, один - со скоростью 3 км/ч, второй -
5 км/ч. Запишите формулой расстояние между ними через t ч. Упростите её. Какой смысл имеет число 2 в этой формуле?
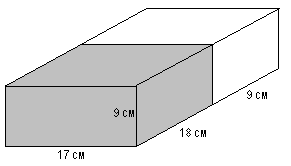
Прямоугольный параллелепипед разделен на две части. Найдите:
а) объём всего параллелепипеда и объёмы его частей. Сравните сумму объёмов частей с объёмом всего
параллелепипеда;
б) общую площадь всех граней параллелепипеда и площади всех граней его частей. Почему сумма этих
площадей не равна общей площади всех граней параллелепипеда? |
 |
Лист картона площадью 600 см2 расчертили на 5 одинаковых полосок, а затем каждую полоску разделили на 8 равных частей.
Объясните смысл выражений (600:5):8 и 600:(5*8) и сделайте вывод об их значениях. Какое свойство иллюстрирует эта задача?
Без подсчёта по рисунку определите, чётное или нечётное количество учеников пришло на урок
Напишите ряд чисел, кратных 25. Обратите внимание на две последние цифры этого числа. Сформулируйте признак делимости на 25.
Докажите без использования таблицы простых чисел, что число составное:
а) 33; б) 54;
в) 93;
г) 315; д) 1020.
Докажите без использования таблицы простых чисел, что число простое:
а) 3; б) 13;
в) 23; г) 31.
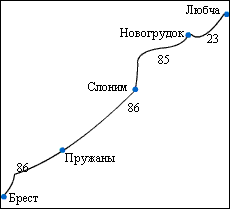
Путь от Любчи до Бреста автобус, двигаясь равномерно, проехал за 4 ч. Докажите истинность утверждения:
а) на путь до Новогрудка автобус затратил менее получаса;
б) на путь до Слонима автобус затратил более полутора часов;
в) на путь до Пружан автобус затратил больше чем 2 ч 30 мин;
г) на путь до Новогрудка автобус затратил меньше чем 20 мин;
д) на путь до Пружан автобус затратил больше чем 2 ч 45 мин. |
 |
Докажите, что число данное составное:
а) 95; б) 1206;
в) 267; г) 1929;
д) 1661; е) 3997.
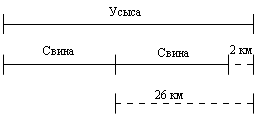
На схеме, показанной на рисунке 5, показаны связи между длинами Усысы и Свины. Составьте задачу по этой схеме и решите её.
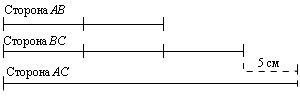
На схеме, приведенной на рисунке 6, показаны связи между сторонами треугольника, периметр которого равен 37 см.
По этой схеме составьте задачу и решите её.
На схеме, приведенной на рисунке 7, показаны связи между углами треугольника. По этой схеме составьте задачу и решите её.
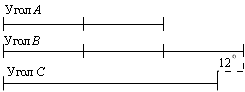Объясните, почему одно число не делится на второе:
а) 2717 на 26; б) 8069 на 21;
в) 4328 на 35; г) 9354 на 170.
Составьте и решите задачу по схеме, где показаны связи между длинами Свислочи и Росси.
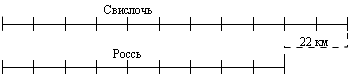В каждом из 379 ящиков лежит не более 125 деталей. Докажите, что есть четыре ящика с одинаковым количеством деталей.
Докажите, что если к любому двузначному числу приписать справа это же число, то получится четырехзначное число, делящееся на 101.
Четными цифрами записано 25 трехзначных чисел. Докажите, что, по крайней мере, 7 из них принадлежат одной сотне.
Нарисуйте в тетради отрезок длиной 6 см. Постройте другой отрезок, составляющий 7/3 его длины. С помощью
рисунка объясните, как неправильную дробь 7/3 заменить смешанной дробью.
Алесь, определяя НОД трех чисел, назвал число 35. Филипп знал о данных числах только то, что их произведение равно
70 000, однако, он сказал, что Алесь ошибся. Прав ли Филипп? Объясните.
В каждом из 75 ящиков лежит не более 17 предметов. Докажите что, по крайней мере, в 5 ящиках
будет лежать одинаковое число предметов.
Встретились два человека, которые не виделись после окончания школы и ничего не знали друг о друге. Между ними произошёл такой
разговор:
- Сколько же лет я тебя не видел и не имел никаких известий?
- А у меня уже дочка.
- Как же её назвали?
- Так же, как и маму.
- И сколько же лет твоей Светлане?
Как один из них узнал имя дочери другого?
Задачи, которые можно установить, не меняя условия
В таблице 2 приведен список соответствующих задач учебника.
>>
Таблица 2
| Раздел |
Список номеров |
| I |
26, 209 , 210, 227, 244,
254, 255, 282, 291
|
| II |
нет |
| III |
558, 581 |
| IV |
635, 656, 733, 766, 775
|
Рассмотрите и осмыслите рисунки.
Двойное неравенство
27 < a < 33
означает
27 < a и
a < 33
28; 29; 30; 31; 32 Рис. 1
|
|
Нестрогое неравенство
b ≤ 11
означает
b < 11 или
b = 11
0; 1; 2; 3; ...; 9; 10; 11 Рис. 2 |
Нестрогое неравенство
c ≥ 47
означает
c = 47 или
c > 47
47; 48; 49; 50; ... Рис. 3
|
|
Двойное неравенство
13 ≤ d < 18
означает
d = 13 или
(13 < d и d < 18
13; 14; 15; 16; 17 Рис. 4 |
Сделайте подробные записи для неравенства
а) 2<k<7;
б) 17>l>12;
в) m≤5; |
|
г) n≥12;
д) 39≤p<43;
е) 58<q≤60; |
|
ж) 26≤r≤30;
з) 19≥s≥13;
и) 14<t<10; |
|
к) 22<u≤23;
л) 31≤v<31;
м) 26≤y≤27; |
Отметьте точку T. Постройте окружность с центром T. Измерьте радиус окружности. Без измерения определите её диаметр.
Идея: линейку привязать к центру окружности, радиус случайный, проверка внутри flash-фильма
Начертите окружность и отметьте на ней три точки X,Y,Z:
а) запишите все дуги, на которые разделили окружность эти точки;
б) сколько всего разных дуг с концами X,Y,Z получилось? Запишите их;
в) сколько всего хорд определяют эти точки? Запишите их.
Начертите угол с вершиной A. На его стороне выберите точки B и C. На отрезке BC отметьте точку D. Проведите луч AD. Запишите
все образовавшиеся углы.
Начертите сектор с радиусом 5 см и углом в:
а) 90о; б) 45о;
в) 180о; г) 225о.
Начертите с помощью угольника три прямых угла в разных расположениях.
Начертите три острых угла в разных расположениях и измерьте их.
Угол BCD равен 26о. Продлите его стороны за вершину C. Найдите величины каждого из образовавшихся углов.
Начертите два равных угла AOB и COD с общей вершиной O. Запишите ещё одну пару равных углов на этом рисунке.
Начертите окружность с центром O радиусом 5 см и её хорду MN длиной 5 см. Проведите диаметр MK. Измерьте углы треугольника MNK.
Найдите его периметр.
На столе лежат карточки, на одной стороне каждой из них написано число или буква. Какие карточки достаточно перевернуть, чтобы
узнать, истинно ли утверждение:
а) если на карточке написана гласная буква, то на соседней слева карточке - чётное число?
б) если на карточке написано чётное число, то на соседней справа карточке - гласная буква?
в) на любых двух соседних карточках написаны число и буква?
Нарисуйте прямоугольник со сторонами 9 см и 6 см. Разделите каждую его сторону на 6 равных отрезков. Какую длину имеют эти
отрезки? Через точки деления проведите отрезки, параллельные сторонам. Какую часть прямоугольника составляет один малый
прямоугольник? Какую часть прямоугольника составляют малые прямоугольники, прилежащие к сторонам?
Постройте в тетради угол, градусная мера которого равна:
а) 90о;
б) 150о; в) 45о; г) 360о;
д) 0о; е) 105о.
Нарисуйте отрезок длиной 6 см. Постройте отрезки, составляющие:
а) 3/4;
б) 11/4; в) 13/4;
г) 21/4; д) 12/4
его длины. По рисунку определите, сколько четвёртых долей содержит каждый из построенных отрезков.
Нарисуйте круг радиусом 5 см. Проведите два радиуса так, чтобы один из полученных секторов составлял
2/7 другого.
| Как разрезать квадрат на 4 одинаковые по форме и по размерам части так, чтобы каждая из них содержала по одному
синему квадратику? |
|
|
К содержанию