
Рисунок 2.1
Электронный учебник "Математика. 4 класс" основан на учебнике Лаготина и Чеботаревского [1], являющегося учебным пособием для четвёртых классов средней школы. Пособие содержит четыре раздела: "Сложение и вычитание нату-ральных чисел", "Умножение и деление натуральных чисел", "Делимость натуральных чисел", "Дроби", разбитых на сорок девять параграфов, каждый из которых содержит теоретический материал и задачи.
В первом разделе систематизируются знания учащихся о записи, сложении и умножении натуральных чисел, решении уравнений и текстовых задач, шкалах и единицах измерения, некоторых геометрических фигурах (точка, прямая, отрезок, угол, окружность, круг), изучается округление чисел, вводятся понятия координатного луча, смежных и вертикальных углов, формула суммы углов треугольника.
Во втором разделе обобщаются и систематизируются знания учащихся об умножении и делении натуральных чисел, вводятся понятие площади и объёма, квадрата и куба числа, прямоугольного параллелепипеда.
В третьем разделе учебника изучаются деление с остатком, разложение числа на множители, признаки делимости на два, три, пять, девять и десять, вводятся понятия наибольшего общего делителя и наименьшего общего кратного.
Четвёртый раздел целиком посвящён понятию и свойствам обыкновенных дробей. В нём вводится понятие обыкновенной дроби, изучаются сравнение обыкновенных дробей и арифметические операции над ними.
2.2.1 Описание курса
В структуре курса "Математика. 4 класс" выделяются два основных раздела: "Теория" и "Задачи". В разделе "Теория" выделены основная часть и приложения.
Основная часть раздела "Теория" содержит весь теоретический материал [1], разбитый на главы и параграфы в соответствии со структурой учебного пособия. Она реализована с помощью языка разметки текста HTML и таблиц стилей CSS (Cascade Style Sheets) [2], [3].
В приложениях содержатся таблицы единиц измерения и простых чисел, приведенные в [1], а также, тренировочные упражнения, реализованные посредством Flash-технологии, которые можно разбить на:Тренировочные упражнения отличаются тем, что проверка правильности ответа осуществляется непосредственно в программе упражнения, и её результаты становятся известными пользователю немедленно. За решение тренировочных заданий не выставляются баллы.
Раздел "Задачи" основан на упражнениях учебного пособия [1]. Все содержащиеся в нём задания проверяются с выставлением баллов и фиксацией их в таблице результатов.
Учебное пособие [1] содержит 921 задачу. С точки зрения особенностей электронной реализации, эти задачи разбиваются на:Существуют задачи, которые нельзя установить на сайт дистанционного обучения в качестве проверяемых упражнений без внесения значительных изменений в условие. В отдельных заданиях от учащихся требуется доказывать утверждения, объяснять приводимые факты или составлять задачи с использованием некоторых числовых данных.
В настоящее время в разделе "Задачи" электронного учебника "Математика. 4 класс" содержится 730 задач группы а) и 106 задач группы b).
Раздел "Задачи" разбит на подразделы в соответствии со структурой учебного пособия [1]. Помимо четырёх подразделов, соответствующих главам учебника (с вложенными подразделами, соответствующими параграфам, в которых и находятся непосредственно упражнения), раздел содержит подраздел "Контрольные упражнения", в котором объединены все задачи, реализованные с применением Flash. В свою очередь, "Контрольные упражнения" содержит несколько подразделов, объединяющих задачи в соответствии с тематикой.
Примеры
№383 В треугольнике один угол втрое больше другого и на 30о больше третьего. Определите углы треугольника.
№532 Определите, делится ли на 9 число:
| а) 792; б) 7864; |
в) 8532; г) 76 318; | д) 90 631; е) 234 562 895; | ж) 785 327; з) 7 564 893. |
№543 Постройте угол в 145о и на его сторонах от вершины отложите отрезки длиной 72 мм и 56 мм. Соедините концы этих отрезков. Получился треугольник. Найдите вычислением третий угол. Проверьте вычисления измерением.
№534 Запишите три натуральных числа, кратных числу 9, которые:
| а) трёхзначные; б) четырёхзначные; |
в) пятизначные; г) шестизначные. |
№ 619 В каждом из 379 ящиков лежит не более 125 деталей. Докажите, что есть четыре ящика с одинаковым количеством деталей.
2.2.2 Стандартные задачи
Стандартные средства установки дают возможность изобразить правильный ответ на вопрос задачи при помощи одного из стандартных полей ввода или комбинации нескольких стандартных полей - поля ввода текста (Edit), поля ввода множества строк (TextArea), выпадающего списка вариантов (ComboBox), скрытого поля (Hidden), флажков выбора нескольких вариантов (CheckBox), флажков выбора одного из нескольких вариантов, или радиокнопок (RadioButton). К стандартным средствам также относятся radio_group (группа радиокнопок), hradio_group (строка радиокнопок), choose (текст с возможностью выделения), classify_table (классификационная таблица), ache (головоломка) и map(рисунок с привязанной картой).[4]
При разработке курса "Математика 4 класс" использовались два стандартных метода установки: стандартный интерфейс для задач с выбором и вводом и интерфейс с созданием собственной формы средствами html. Большинство задач было установлено первым способом. Он является более быстрым, однако, стандартный интерфейс позволяет разместить лишь одно поле ввода (любого типа) в строке, текст в строке может предшествовать полю ввода, но не может следовать за ним. Поэтому, при реализации, например, электронной версии упражнений, содержащих таблицы, удобнее создать собственную форму.
Стандартными средствами были установлены упражнения с одним чётко определённым ответом либо некоторым (небольшим) числом чётко определённых правильных вариантов ответа. К таким задачам относится большинство текстовых задач учебника (не связанных с геометрическими построениями и координатами), числовые выражения, уравнения и неравенства с использованием четырёх арифметических действий, задачи по переводу одних единиц измерения в другие, большинство задач с блоксхемами а также, некоторые геометрические задачи (в которых не было прямого требования строить чертёж или выполнять измерения).
Кроме этого, некоторые задачи, изначально требовавшие от учащихся делать выводы или обосновывать утверждения, были переформулированы и установлены стандартными средствами. В этом случае в условии возникало предложение выбрать один из нескольких вариантов ответа.
Пример
№695. На рисунке представлены дроби 3/8 и 3/4. Какая из дробей больше и во сколько раз? Как получить число 3/4 из числа 3/8?При установке задача была переформулирована. Вид упражнения показан на рисунке 2.1

В некоторых упражнениях, установленных стандартными средствами, даётся образец ввода (в основном - при необходимости вводить в одно поле список значений или указывать единицы измерения). Образец может размещаться в левом вертикальном или верхнем горизонтальном фрейме, а при отсутствии фреймов - ниже условия задачи.
Как упоминалось выше, задачи, установленные стандартными средствами, объединены в темы, соответствующие параграфам учебного пособия [1].
2.2.3 Задачи, установленные с использованием Flash
Упражнения, реализованные с помощью Flash, содержатся в курсе в двух экземплярах. Один размещается в соответствующем параграфе, второй - в разделе "Контрольные упражнения", объединяющем все задачи этого типа.
В разделе "Контрольные упражнения" выделены тематические подразделы:
В окне упражнения при выполнении задачи появляется форма фильма Flash. Ниже неё расположена кнопка "Отправить". Если не оговорено обратное, для отправки решения достаточно нажать на эту кнопку (в некоторых упражнениях требуется предварительно нажать на кнопку внутри фильма).
1) Задачи на восстановление примеров, как правило, имеют вид "Замените звёздочки цифрами..." (рисунок 2.2)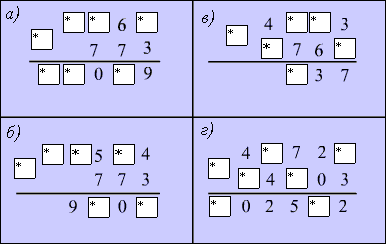
2) В задачах на измерения требуется с помощью линейки, транспортира, угольника или циркуля, изображённых на экране, измерять отрезки или углы (рисунок 2.3).

В некоторых задачах измерительные инструменты можно перемещать. Чтобы перетащить инструмент, нужно навести на него курсор, нажать на левую кнопку мыши и, не отпуская её, передвинуть курсор в нужную точку. Вместе с курсором сместится и инструмент.
В некоторых задачах измерительные инструменты можно вращать. Для этого используются поле ввода (задаётся угол поворота) и кнопки (рисунок 2.3). Линейка вращается вокруг своего левого верхнего угла, угольник - вокруг вершины внешнего угла, транспортир - вокруг нижней точки центрального штриха, циркуль - вокруг нижней точки левой "иглы".
При работе с инструментом "циркуль" (рисунок 2.4) для изменения раствора циркуля используются кнопки со стрелками, размещённые в верхней части инструмента. Примером упражнения, в котором используется циркуль, является задача №113, в которой требуется по рисунку с помощью циркуля найти равные отрезки. (Открыть фильм в новом окне) |
Рисунок 2.4 |
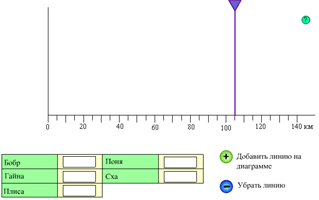
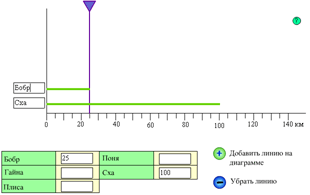
3) В упражнениях на работу с координатным лучом область построения - имитация страницы тетради (рисунок 2.6). На практике в большинстве таких задач можно размещать точки лишь на одной предопределённой прямой.
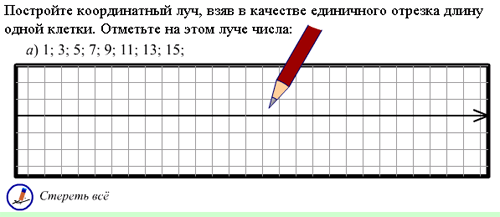
При помещении курсора мыши в область построения на экране появится карандаш. После щелчка мышью на координатном луче появляется точка, а выше или ниже неё - поле ввода. В отдельных задачах возникает два поля ввода (рисунок 2.7). В этом случае числовые подписи точек размещаются ниже координатного луча, а буквенные обозначения - выше. Открыть фильм в новом окне

Удаление неверных построений осуществляется посредством кнопок. Как правило, удаляются все построенные точки (иногда присутствует кнопка "Стереть последнее").
4) В упражнениях на построение геометрических фигур областью построения является прямоугольник-"страница". При размещении курсора мыши в области построения на экране появляется карандаш (рисунок 2.6). Щелчок мышью вызовет появление точки и поля ввода подписи к ней. Рисование отрезков и окружностей осуществляется посредством кнопок по следующим схемам:
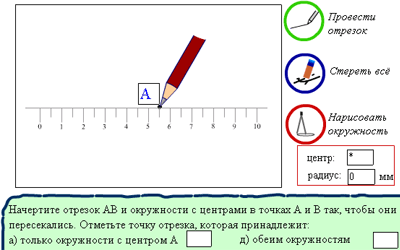
5) Среди задач с дробями можно выделить два основных типа: задачи, содержащие выражения с дробями и задачи на перечисление дробей. Упражнения первой группы обладают достаточно простым интерфейсом - пользователь просто заполняет поля ввода.
Для упражнений второй группы (рисунок 2.9) характерна неопределённость количества полей ввода. Первоначально видимо лишь одно, добавление и удаление полей ввода осуществляются с помощью кнопок.

6) В задачах, объединённых в теме "Разложение на множители", как правило, требуется представить число в виде произведения, найти все его делители или перечислить общие делители нескольких чисел. Большинство таких задач обладают стандартным интерфейсом. В задачах рассматриваемой группы, как правило, даётся образец ввода с указанием разделителя (при перечислении) и пояснением возможных спорных моментов. Образец ввода обычно размещается в нижней части фильма.
7) Упражнения, не вошедшие ни в один из подразделов, достаточно разнообразны. Среди них встречаются как стандартные задачи с нетипичным оформлением (№№29, 226, 228, 452, 517, 750), которые не удалось объединить в особый подраздел "Контрольных упражнений" из-за малочисленности, так и задачи на сообразительность (№№34, 35, 350, 409, 480, 711).
Примеры
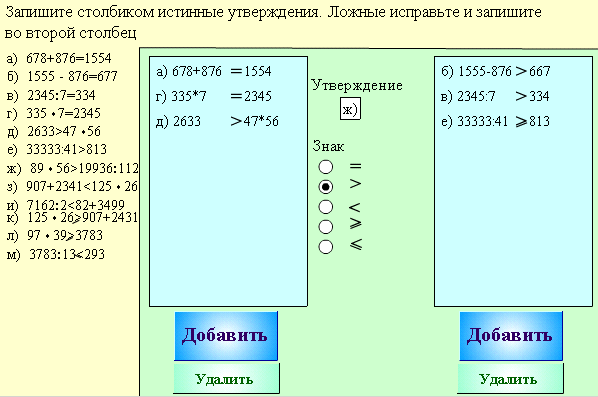


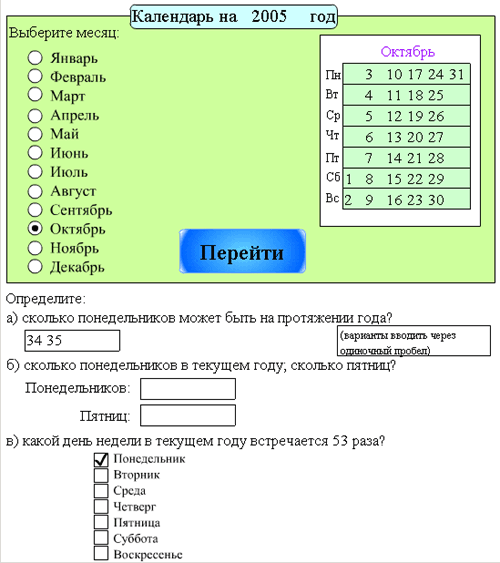
2.2.4 Тренировочные задания
Ссылка на перечень тренировочных заданий находится в подразделе "Приложения" раздела "Теория". Выделяются четыре подраздела тренировочных заданий:
1) Задачи на восстановление примеров основаны на номерах учебника. Интерфейс упражнений выполнен одинаково и похож на интерфейс соответствующих проверяемых задач.
2) Среди задач, требующих заполнения таблиц, встречаются как основанные на конкретных номерах учебника, так и смоделированные на основе изучаемого материала. В условии упражнений второго типа числа определяются с помощью генератора случайных чисел при каждом запуске приложения.
Пример
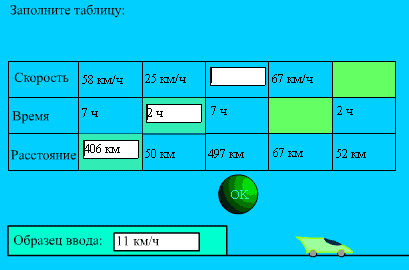
В задании требуется указать число и единицы измерения. Проверка правиль-ности осуществляется после нажатия на кнопку "ОК". Если ячейка заполнена правильно, возникает следующее поле ввода, а кнопка "ОК" перемещается вправо (к следующему столбцу таблицы). Если ячейка заполнена неправильно, рядом появ-ляется надпись "Неверно". После заполнения всех ячеек таблицы появляется надпись "Задание выполнено".
3) Задачи с блоксхемами
В учебнике математики четвёртого класса [1] содержится ряд номеров вида "Какое число будет получено на выходе вычислительной
машины, если на входе было подано число a?" или "Какое число было подано на вход машины, если на выходе получено число
b?". При этом, ход вычислений задается посредством блоксхемы.
В тренировочных задачах числа, подаваемые на вход или получаемые на выходе, задаются случайно. Для одной и той же блоксхемы может существовать до трёх типов заданий:
При этом, в задачах второго вида ответ, вообще говоря, может отсутствовать или не быть единственным, что необходимо учесть.
Пример
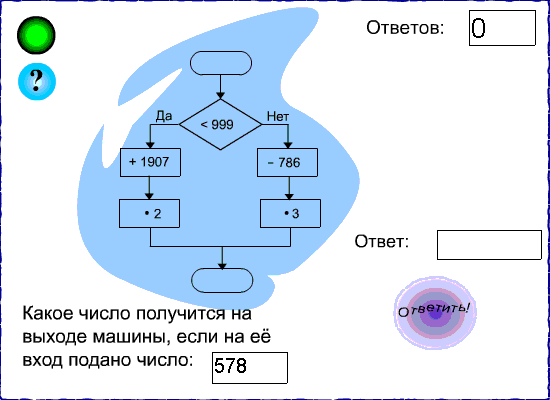
За каждое правильное число, введенное в поле "Ответ", пользователь получает один балл.
4) В учебном пособии [1] встречается несколько игровых задач, в которых от учащегося требуется указать стратегию выигрыша. На основании этих задач созданы игровые задания курса.
Пример
Условие задачи. Познакомьтесь с игрой "Назови 100" . В неё играют вдвоём. Первый называет число от 1 до 9, второй прибавляет к названному своё число от 1 до 9 и т.д. Выигрывает тот, кто первым получит 100. Как выиграть?
Соответствующее приложение реализует саму игру:
При запуске приложения игры пользователю предлагается выбрать, кому принадлежит право первого хода. Затем игроки поочерёдно называют числа, пока не будет достигнут результат.